FFT: PHƯƠNG TRÌNH VÀ LỊCH SỬ

Được đặt tên theo nhà toán học người Pháp Jean - Baptiste Joseph Fourier cuối thế kỷ 18, biến đổi Fourier là một phép toán biến đổi tín hiệu từ miền thời gian (không gian) sang miền tần số. Theo định lý Fourier, một tín hiệu là sự hợp thành của một số hàm điều hòa với biên độ, tần số và pha cho trước. Dạng chuỗi Fourier cho tín hiệu tuần hoàn, x(t):

Với sóng sin, chỉ có một hệ số. Tuy nhiên, nếu tín hiệu chứa một số lượng vô hạn các tần số, chẳng hạn như trong trường hợp sóng vuông lý tưởng, một kết quả hữu hạn N  sẽ dẫn đến lỗi. Hình 1 và 2 là tín hiệu gốc được biểu diễn theo chuỗi Fourier với N = 3 (tín hiệu màu xanh lục) và N = 15 (tín hiệu màu xanh lam). Như chúng ta thấy, độ chính xác của phép biến đổi phụ thuộc vào bản chất của tín hiệu và số số hạng trong chuỗi.

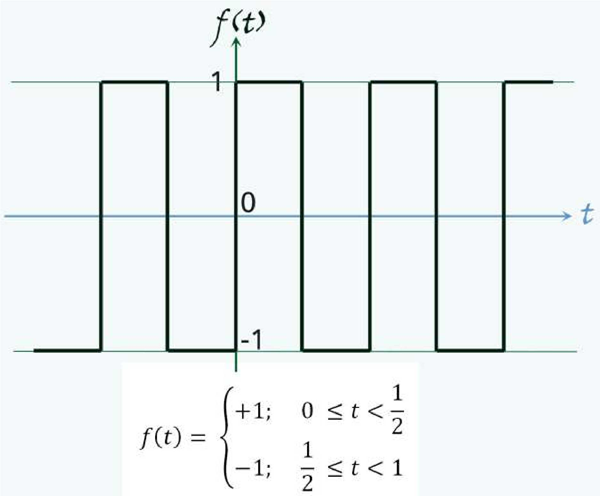
Hình 1. Hàm sóng vuông lý tưởng

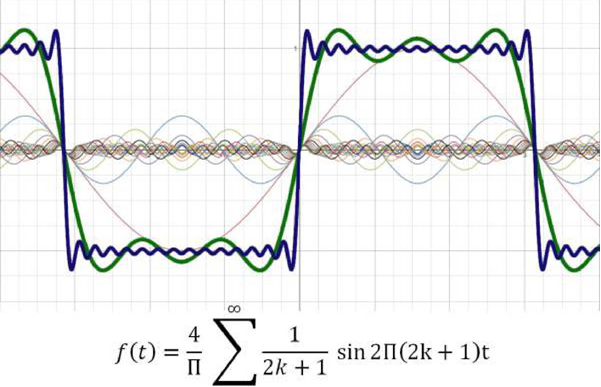
Hình 2. Dạng chuỗi Fourier của sóng vuông với N=3 và N=15

Tuy nhiên, hầu hết các tín hiệu không tuần hoàn. Các tín hiệu không tuần hoàn không có chuỗi Fourier. Thực tế này làm Fourier thất vọng, ông phải mất gần 20 năm để phát triển một công thức chung có thể hoạt động cho bất kỳ hàm nào. Bây giờ, mọi tín hiệu đều có thể được chuyển từ miền thời gian sang miền tần số theo phương trình sau đây:

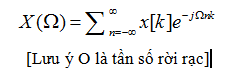
Phương trình này không chỉ đơn thuần là toán học. Nó mô tả các khối cấu thành các tín hiệu, và từng khối riêng biệt. Tức là, cho dù các thành phần của tín hiệu dù nhỏ hay lớn, chúng đều sẽ xuất hiện trong danh sách thành phần được cung cấp bởi phép biến đổi. Xét một tín hiệu phức tạp bao gồm một sóng sin và một hàm sinc như trong Hình 3.

Hình 3. Biểu diễn một tín hiệu phức tạp bao gồm một sóng sin và một hàm sinc trên miền thời gian

Biểu diễn tín hiệu trên miền thời gian không có gì hữu ích. Phổ tần số biên độ (Hình 4) cho thấy rõ ràng thành phần của nó. Lưu ý rằng những thành phần mong muốn có thể được phân tích một cách riêng biệt. Đó là khả năng của phép biến đổi.

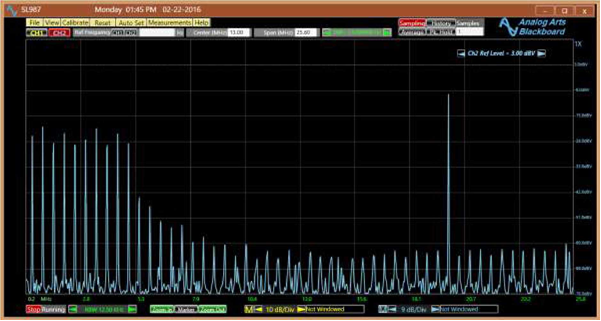
Hình 4. Phổ tần của một tín hiệu phức tạp bao gồm một sóng sin và một hàm sinc

Công thức tìm được thực sự  tuyệt vời. Nhưng sẽ phải thực hiện việc biến đổi mãi mãi. Số lượng phép tính cần thiết để xử lý phương trình này tỉ lệ với  Rõ ràng, vấn đề trở nên phức tạp khi  càng lớn vì số lượng các phép tính tăng lên nhanh chóng đến mức không thực tế. Các máy tính đầu tiên đã mất hàng trăm giờ để thực hiện một phép biến đổi đơn giản theo các tiêu chuẩn hiện nay. Do đó, kể từ năm 1805 đã có những nỗ lực để nâng cao hiệu quả của thuật toán. Cùng năm đó, Carl Friedrich Gauss đã phát minh ra một phương pháp biến đổi Fourier hiệu quả. Tuy nhiên, nó vẫn không rõ ràng trong 160 năm nữa.

Năm 1965, James Cooley của IBM và John Tukey của Princeton đã khám phá ra thuật toán này và phổ biến nó. Việc làm của họ làm giảm đáng kể số lượng phép tính. Sự suy giảm đặc biệt đáng chú ý khi  bằng lũy thừa của 2. Trong trường hợp này, số lượng phép tính tỉ lệ với  Thuật toán được gọi là FFT ngay sau khi được giới thiệu. Nó lập tức tạo nên sự cách mạng trong biến đổi Fourier của các tín hiệu. Với 64000 điểm FFT, thuật toán này nhanh gấp 4000 lần so với phương pháp ban đầu. Nó đã có một số sửa đổi kể từ khi phát hiện ra. Và vào tháng 1 năm 2000, nó được đưa vào Top 10 Thuật toán của thế kỷ 20.

Với sự ra đời của việc xử lý tín hiệu số, FFT được nâng lên một tầm quan trọng mới. Một số công ty như Texas Instruments và Analog Devices giới thiệu bộ xử lý FFT chuyên biệt. Một khi tín hiệu thoát ra khỏi miền tương tự thông qua một bộ chuyển đổi tươn g tự sang số, các khả năng là vô tận.

Hình 5. Tín hiệu từ Đài quan sát Arecibo ở Puerto Rico được phân tích để tìm kiếm thông tin của người ngoài hành tinh

Nhiều ứng dụng được hưởng lợi từ FFT, đặc biệt là lĩnh vực truyền thông. Radar, điện thoại tế bào, xử lý tiếng nói, và SETI (tìm kiếm trí tuệ ngoài trái đất) là một vài ứng dụng sử dụng rộng rãi FFT.

Các ứng dụng của FFT bao quanh mọi lĩnh vực của cuộc sống. Đó có thể là các thiết bị giám sát, một bộ tổng hợp hoặc một bộ phân tích tín hiệu để phép biến đổi Fourier có thể được ứng dụng. Ngày nay thì hầu hết các tín hiệu đều không thể được ứng dụng nếu không có phép biến đổi Fourier.

Nguồn: RSI